💡 A sequence (of real numbers) is a transformation

$$a:\mathbb{N}⟶\mathbb{R}$$

We write $a_n$ instead of $a(n)$ and denote a series with $(a_n{)}_{n\ge 1}$.

📌 Let $(a_n{)}_{n_{\ge }1}$ a sequence. Then there exists at most one real number $l\in \mathbb{R}$ with the property:

$$\forall ϵ>0\text{the set}\{n\in \mathbb{N}|a_n\notin (l-ϵ,l+ϵ)\}\text{is finite}.$$

💡 A sequence $(a_n{)}_{n\ge 1}$ is called convergent if there exists $l\in \mathbb{R}$ such that $\forall ϵ>0$ the set

$$\{n\in {\mathbb{N}}^{\ast }|a_n\notin (l-ϵ,l+ϵ)\}$$

is finite. By lemma, if such a number $l$ exists it is uniquely determined, and is denoted

$$\underset{n\to \infty }{\lim }{a}_n$$

and is called the limit of the sequence $(a_n{)}_{n\ge 1}$.

💡 In other words, a sequence $(a_n)$ has a limit $L$ if and only if there exist only a finite number of elements of the sequence outside an arbitrarily large surrounding area of $L$ ($(L-ϵ,L+ϵ)$).

📌 Let $(a_n{)}_{n\ge 1}$a sequence. The following statements are equivalent:

• $\ast (a_n{)}_{n\ge 1}$ converges to $l={\lim }_{n\to \infty }{a}_n$*

• $\ast \forall ϵ>0\exists N\ge 1$, such that*

  $$|a_n-l|<ϵ\forall n\ge N.$$

📖 Let $(a_n{)}_{n\ge 1}$ and $(b_n{)}_{n\ge 1}$ convergent sequences with $a={\lim }_{n\to \infty }{a}_n$, $b={\lim }_{n_{\to }\infty }{b}_n$.

• Then $(a_n+b_n{)}_{n\ge 1}$ is convergent and ${\lim }_{n\to \infty }(a_n+b_n)=a+b$.
• Then $(a_n\cdot b_n{)}_{n\ge 1}$ is convergent and ${\lim }_{n\to \infty }(a_n\cdot b_n)=a\cdot b.$
• Assume, that $b_n\ne 0\forall n\ge 1$ and $b\ne 0$. Then $(\frac{a_n}{b_n}{)}_{n\ge 1}$ is convergent and ${\lim }_{n\to \infty }\left(\frac{a_n}{b_n}\right)=\frac{a}{b}.$
• If there exists $K\ge 1$ with $a_n\le b_n\forall n\ge K$ then it follows that $a\le b$.

📖 “Sandwich Theorem”, Squeeze Theorem:

Let $(a_n)$, $(b_n)$ be two convergent sequences with the same limit $L\in \mathbb{R}$. Let $k\in \mathbb{N}$ and $(c_n)$ be a sequence with the property that

$$a_n\le c_n\le b_n\forall n>k.$$

Then $c_n$ converges to $L$.

💡 Monotonically increasing/decreasing:

• $(a_n{)}_{n\ge 1}$ is monotonically increasing if:

  $$a_n\le a_{n+1}\forall n\ge 1.$$

• $(a_n{)}_{n\ge 1}$ is monotonically decreasing if:

  $$a_{n+1}\le a_n\forall n\ge 1.$$

📖 Weierstrass’ Theorem (Monotony Convergence Theorem):

• Let $(a_n{)}_{n\ge 1}$ be monotonically increasing and bounded from above. Then $(a_n{)}_{n\ge 1}$ converges towards

  $$\underset{n\to \infty }{\lim }{a}_n=\sup \{a_n|n\ge 1\}.$$

• Let $(a_n{)}_{n\ge 1}$ be monotonically decreasing and bounded from below. Then $(a_n{)}_{n\ge 1}$ converges towards

  $$\underset{n\to \infty }{\lim }{a}_n=\inf \{a_n|n\ge 1\}.$$

💡 In other words, the above theorem say that if a sequence is monotonically in-/decreasing and it is bounded from above/below respectively, then it is a convergent sequence.

💡 The sequence $(1+\frac{1}{n}{)}^n$, $n\ge 1$ converges. The limit is

$$e=\underset{n\to \infty }{\lim }(1+\frac{1}{n}{)}^n,$$

Euler’s number $e=2.71828\dots$.

The sequence can be applied in compounding interest rates, for example: Assume you take out a loan for 1 CHF, with 100% yearly interest rate. When compounding once a year ($n=1$), well, you owe 2 CHF as given by $(1+1{)}^1=2$. When compounding twice a year ($n=2$) you owe 2.25 CHF as given by $(1+\frac{1}{2}{)}^2=2.25$.

Every month ($n=12$): $(1+\frac{1}{12}{)}^{12}=2.613\dots$.

Every day ($n=365$): $(1+\frac{1}{365}{)}^{365}=2.714\dots$

At max, you will owe $e$ CHF.

💡 A sequence is called bounded if the set of elements of the sequence $\{a_n|n\in \mathbb{N}\}$ is bounded.

💡 A sequence $(a_n{)}_{n\ge 1}$ is called a zero-sequence if $\lim a_n=0.$

💡 Every convergent sequence is bounded, but not necessarily the other way around.

💡 The sequence $x_n=q^n$ is called a geometric sequence. It holds for all $n$ that $\frac{x_{n+1}}{x_n}=q$.

📌 (Bernoulli’s Inequality).

$$(1+x{)}^n\ge 1+n\cdot x\forall n\in \mathbb{N},x>-1$$

💡 Fixed-point Interation:

Used for recursive sequences.

Example: $\sqrt{c}$ is the solution of the equation

$$\begin{array}{rl}& x^2=c\\ ⟺& x^2=\frac{c}{2}+\frac{c}{2}=\frac{x^2}{2}+\frac{c}{2}\\ ⟺& x=\frac{x}{2}+\frac{c}{2x}=\frac{1}{2}(x+\frac{c}{x})\end{array}$$

Let $f(x)=\frac{1}{2}(x+\frac{c}{x})$. That means that $x=f(x)$. This equation is called a fixed-point equation for the function $f(x)=\frac{1}{2}(x+\frac{c}{x})$.

The corresponding fixed-point iteration is given by $x_{n+1}=f(x_n)=\frac{1}{2}(x_n+\frac{c}{x_n})$.

💡 Limes superior and limes inferior ($\mathrm{limsup},\mathrm{liminf}$):

Let $(a_n)$ be a bounded sequence. As a consequence of Weierstrass’ theorem we can define two monotonous and convergent sequences $(b_n{)}_{n\ge 1}$ and $(c_n{)}_{n\ge 1}$ from $(a_n{)}_{n\ge 1}$.

Let $n\ge 1$. For every $n$ we define

$$\begin{array}{rl}{b}_n& =\inf \{a_k|k\ge n\}\\ & =\inf \{a_n,a_{n+1},\dots \}\end{array}$$

$$\begin{array}{rl}{c}_n& =\sup \{a_k|k\ge n\}\\ & =\sup \{a_n,a_{n+1},\dots \}\end{array}$$

For every $n$, the set

$$\begin{array}{rl}{A}_n& =\{a_k|k\ge n\}\\ & =\{a_n,a_{n+1},\dots \}\subset \{a_1,\dots \}\end{array}$$

is also bounded and it holds that

$$A_{n+1}\subset A_n$$

• $b_n=\inf A_n\le \sup A_n=c_n$
• $\inf A_n\le \inf A_{n+1}$, i.e., $b_n\le b_{n+1}$ from which follows that $b_n$ grows as $n$ grows
• $\sup A_{n+1}\le \sup A_n$, i.e., $c_{n+1}\le c_n$ from which follows that $c_n$ shrinks as $n$ grows

The two sequences $b_n$ and $c_n$ converge by Weierstrass’ theorem.

We define

$$\underset{n\to \infty }{\lim }{b}_n=\mathrm{liminf}{a}_n$$

as the limes inferior of $a_n$.

We define

$$\underset{n\to \infty }{\lim }{c}_n=\mathrm{limsup}{a}_n$$

as the limes superior of $a_n$.

💡 For the above definition of limes superior and inferior it holds that $\mathrm{liminf}{a}_n\le \mathrm{limsup}{a}_n$ as $b_n\le c_n$.

📌 $(a_n{)}_{n\le 1}$ converges if and only if $(a_n{)}_{n\ge 1}$ is bounded and $\mathrm{liminf}{a}_n=\mathrm{limsup}{a}_n$.

📖 The Cauchy Criterion

The sequence $(a_n{)}_{n\ge 1}$ converges if and only if

$$\forall ϵ>0\exists N\ge 1\text{such that}|a_n-a_m|<ϵ\forall n,m\ge N.$$

💡 A sequence $(a_n)$ is called a Cauchy sequence if there exists a $N$ for all $ϵ>0$ such that for all $m,n\ge N$ it holds that $|a_n-a_m|<ϵ$.

💡 Every Cauchy sequence is bounded.

💡 Every convergent sequence is a Cauchy sequence.

💡 Every Cauchy sequence is convergent.

💡 Every sequence that is not a Cauchy sequence is divergent.

💡 A closed interval is a subset $I\subseteq \mathbb{R}$ of the form

1. $[a,b],a\le b,a,b\in \mathbb{R}$
2. $[a,+\infty ),a\in \mathbb{R}$
3. $(-\infty ,a],a\in \mathbb{R}$
4. $(-\infty ,+\infty )=\mathbb{R}$

We define the length $\mathcal{L}(I)$ of the interval as

$$\begin{array}{rlr}\mathcal{L}(I)& =b-a& \text{in the first case}\\ \mathcal{L}(I)& =+\infty & \text{in the other cases}.\end{array}$$

Clearly $\mathcal{L}(I)\ge 0$. The closed interval is a bounded subset of $\mathbb{R}$ if and only if $\mathcal{L}(I)<+\infty$.

📖 (Cauchy-Cantor.)

Let $\dots \subseteq I_{n+1}\subseteq I_n\subseteq \dots \subseteq I_2\subseteq I_1$ be a sequence of closed intervals with $\mathcal{L}(I_1)<+\infty$.

Then it holds that

$$\bigcap _{n\ge 1}{I}_n\ne \varnothing .$$

If also ${\lim }_{n\to \infty }\mathcal{L}(I_n)=0$ then ${\bigcap }_{n\ge 1}{I}_n$ contains exactly one point.

💡 A subsequence of a sequence $(a_n{)}_{n\ge 1}$ is a sequence $(b_n{)}_{n\ge 1}$ where

$$b_n=a_{l(n)}$$

and $l:\mathbb{N}⟶\mathbb{N}$ is a transformation with the property

$$l(n)<l(n+1)\forall n\ge 1.$$

📖 (Bolzano-Weierstrass.)

Every bounded sequence contains a convergent subsequence.

💡 Let $(a_n{)}_{n\ge 1}$ be a bounded sequence. Then the following holds for every convergent subsequence $(b_n{)}_{n\ge 1}$:

$$\underset{n\to \infty }{\mathrm{liminf}}{a}_n\le \underset{n\to \infty }{\lim }{b}_n\le \underset{n\to \infty }{\mathrm{limsup}}{a}_n.$$

Also, there exist two subsequences of $(a_n{)}_{n\ge 1}$ that approach ${\mathrm{liminf}}_{n\to \infty }{a}_n$ respectively ${\mathrm{limsup}}_{n\to \infty }{a}_n$ in their limit.

💡 A sequence in ${\mathbb{R}}^d$ is a transformation

$$a:\mathbb{N}⟶{\mathbb{R}}^d.$$

We write $a_n$ instead of $a(n)$ and denote a series with $(a_n{)}_{n\ge 1}$.

💡 A sequence $(a_n{)}_{n\ge 1}$ in ${\mathbb{R}}^d$ is called convergent, if there exists $a\in {\mathbb{R}}^d$ such that:

$$\forall ϵ>0\exists N\ge 1\text{with}||a_n-a||<ϵ\forall n\ge N.$$

If such a number $a$ exists it is uniquely determined, and is denoted

$$\underset{n\to \infty }{\lim }{a}_n=a.$$

and is called the limit of the sequence $(a_n{)}_{n\ge 1}$.

Let $(a_{n,1},a_{n,2},\dots ,a_{n,d})$ be the coordinates of $a_n$.

📖 Let $b=(b_1,\dots ,b_d)$. The following statements are equivalent:

1. ${\lim }_{n\to \infty }{a}_n=b$
2. ${\lim }_{n\to \infty }{a}_{n,j}=b_j\forall 1\le j\le d$.

💡 Let $x=(x_1,\dots ,x_d)$. Then it holds $\forall 1\le j\le d$ that:

$$x_j^2\le \sum _{i=1}^d{x}_i^2\le d\cdot \underset{1\le i\le d}{\max }{x}_i^2.$$

From which it follows that:

$$|x_j|\le ||x||\le \sqrt{d}\cdot \underset{1\le i\le d}{\max }|x_i|.$$

💡 A convergent sequence $(a_n{)}_{n\ge 1}$ in ${\mathbb{R}}^d$ is bounded. That means:

$$\exists R\ge 0\text{with}||a_n||\le R\forall n\ge .1$$

📖 Cauchy-Sequence

1. A sequence $(a_n{)}_{n\ge 1}$ converges if and only if it is a Cauchy-sequence:

$$\forall ϵ>0\exists N\ge 1\text{with}||a_n-a_m||<ϵ\forall n,m\ge N.$$

1. Every bounded sequence has a convergent subsequence.

💡 Let $(a_n{)}_{n\ge 1}$ be a sequence in $\mathbb{R}$ or $\mathbb{C}$. The notion of converge of the series

$$"\sum _{k=1}^{\infty }{a}_k"$$

is based on the sequence $(S_n{)}_{n\ge 1}$ of partial sums:

$$S_N=\sum _{k=1}^n{a}_k.$$

💡 The series

$$"\sum _{k=1}^{\infty }{a}_k"$$

is convergent, if the sequence $(S_n{)}_{n\ge 1}$ of partial sums converges. In this case we define:

$$\sum _{k=1}^{\infty }{a}_k=\underset{n\to \infty }{\lim }{S}_n.$$

💡 (Geometric series.)

Let $q\in \mathbb{C}$ with $|q|<1$. Then ${\sum }_{k=0}^{\infty }{q}^k$ converges towards:

$$\sum _{k=0}^{\infty }{q}^k=\frac{1}{1-q}.$$

💡 (Harmonic series.)

The series

$$\sum _{n=1}^{\infty }\frac{1}{n}$$

diverges.

📖 Let ${\sum }_{k=1}^{\infty }{a}_k$ and ${\sum }_{j=1}^{\infty }{b}_j$ be convergent series, and let $\alpha \in \mathbb{C}$.

1. Then ${\sum }_{k=1}^{\infty }(a_k+b_k)$ is convergent and ${\sum }_{k=1}^{\infty }(a_k+b_k)=\left({\sum }_{k=1}^{\infty }{a}_k\right)+\left({\sum }_{k=1}^{\infty }{b}_k\right)$.
2. Then ${\sum }_{k=1}^{\infty }\alpha \cdot a_k$ is convergent and ${\sum }_{k=1}^{\infty }\alpha \cdot a_k=\alpha \cdot {\sum }_{k=1}^{\infty }{a}_k$.

📖 (Cauchy Criterion.)

The series ${\sum }_{k=1}^{\infty }{a}_k$ converges if and only if:

$$\forall ϵ>0\exists N\ge 1\text{with}\left|\sum _{k=n}^m{a}_k\right|<ϵ\forall m\ge n\ge N.$$

📖 Let ${\sum }_{k=1}^{\infty }{a}_k$ be a series with $a_k\ge 0\forall k\in \mathbb{N}$. The series ${\sum }_{k=1}^{\infty }{a}_k$ converges if and only if the sequence $(S_n{)}_{n\ge 1}$, $S_n={\sum }_{k=1}^n{a}_k$ of partial sums is bounded from above.

📎 (Comparison theorem.)

Let ${\sum }_{k=1}^{\infty }{a}_k$ and ${\sum }_{k=1}^{\infty }{b}_k$ be series with:

$$0\le a_k\le b_k\forall k\ge 1.$$

Then all of the following hold:

$$\begin{array}{rl}\sum _{k=1}^{\infty }{b}_k\text{is convergent}& ⟹\sum _{k=1}^{\infty }{a}_k\text{is convergent},\\ \sum _{k=1}^{\infty }{a}_k\text{is divergent}& ⟹\sum _{k=1}^{\infty }{b}_k\text{is divergent}.\end{array}$$

These implications also hold when there exists $K\ge 1$ such that:

$$0\le a_k\le b_k\forall k\ge K.$$

💡 The series ${\sum }_{k=1}^{\infty }{a}_k$ is called absolutely convergent, if

$$\sum _{k=1}^{\infty }|a_k|$$

is convergent.

📖 An absolutely convergent series ${\sum }_{k=1}^{\infty }{a}_k$ is also convergent and it holds that:

$$\left|\sum _{k=1}^{\infty }{a}_k\right|\le \sum _{k=1}^{\infty }|a_k|.$$

📖 (Leibniz 1682).

Let $(a_n{)}_{n\ge 1}$ be monotonically decreasing with $a_n\ge 0\forall n\ge 1$ and ${\lim }_{n\to \infty }{a}_n=0.$ Then

$$S=\sum _{k=1}^{\infty }(-1{)}^{k+1}{a}_k$$

converges and it holds that:

$$a_1-a_2\le S\le a_1.$$

💡 A series ${\sum }_{n=1}^{\infty }{a}_n^{\prime }$ is called a rearrangement of ${\sum }_{n=1}^{\infty }{a}_n$ if there exists a bijective transformation

$$\varphi :\mathbb{N}⟶\mathbb{N}$$

such that

$$a_n^{\prime }=a_{\varphi (n)}.$$

📖 (Riemann’s Rearrangement Theorem).

Let ${\sum }_{k=1}^{\infty }{a}_k$ be a conditionally convergent series (a series which is convergent but not absolutely convergent). Then, for every $A\in \mathbb{R}\cup \{\infty \}$ there exists a rearrangement of the series which converges towards $A$.

📖 (Dirichlet 1837).

If ${\sum }_{k=1}^{\infty }{a}_k$ converges absolutely, then every rearrangement of the series has the same limit.

📖 (Ratio test, Cauchy 1821).

Let $(a_n{)}_{n\ge 1}$ with $a_n\ne 0\forall n\ge 1.$ If

$$\underset{n\to \infty }{\mathrm{limsup}}\frac{|a_{n+1}|}{|a_n|}<1$$

then the series ${\sum }_{n=1}^{\infty }{a}_n$ converges absolutely.

If

$$\underset{n\to \infty }{\mathrm{liminf}}\frac{|a_{n+1}|}{|a_n|}>1$$

then the series diverges.

💡 The exponential function

We define the exponential function $\exp (z)$ as:

$$\exp (z)=1+z+\frac{z^2}{2!}+\frac{z^3}{3!}+\dots =\sum _{i=0}^{\infty }\frac{z^i}{i!}$$

(Note: this is a Taylor series expansion of $e^z$)

📖 (Root test, Cauchy 1821).

1. If

   $$\underset{n\to \infty }{\mathrm{limsup}}\sqrt[n]{|a_n|}<1$$

   then ${\sum }_{n=1}^{\infty }{a}_n$ converges absolutely.

2. If

   $$\underset{n\to \infty }{\mathrm{limsup}}\sqrt[n]{|a_n|}>1$$

   then ${\sum }_{n=1}^{\infty }{a}_n$ and ${\sum }_{n=1}^{\infty }|a_n|$ diverge.

📎 Let $(c_k{)}_{k\ge 0}$ be a series (in $\mathbb{R}$ or $\mathbb{C}$). If ${\mathrm{limsup}}_{k\to \infty }\sqrt[k]{|c_k|}$ exists, we define

$$\rho =\{\begin{array}{ll}+\infty & \text{if}{\mathrm{limsup}}_{k\to \infty }\sqrt[k]{|c_k|}=0,\\ \frac{1}{{\mathrm{limsup}}_{k\to \infty }\sqrt[k]{|c_k|}}& \text{if}{\mathrm{limsup}}_{k\to \infty }\sqrt[k]{|c_k|}>0.\end{array}$$

The Power series

$$\sum _{k=0}^{\infty }{c}_k{z}^k$$

converges absolutely for all $|z|<\rho$ and diverges for all $|z|>\rho$.

💡 Let $s>1$ and

$$\zeta (s)=\sum _{n=1}^{\infty }\frac{1}{n^s}.$$

The function $\zeta (s)$ is called the Riemann zeta function.

The uniquely determined complex analytic continuation of $\zeta (s)$, which extends the domain of $\zeta (s)$ to all of $\mathbb{C}$, is the function underlying the Riemann hypothesis conjecturing that all roots of the function have a Real part of exactly 0.5, which is currently an unsolved millenium problem.

💡 Double summation

Consider the following:

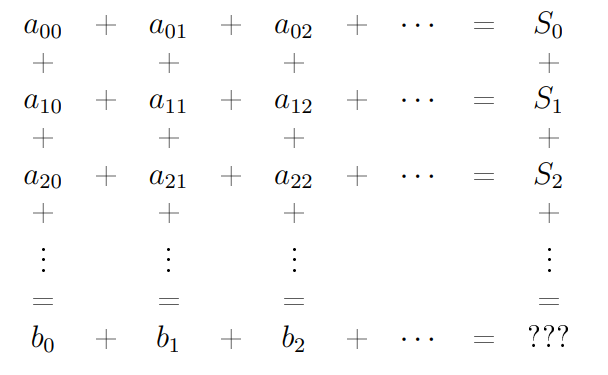
Given a double sequence $(a_{ij}{)}_{i,j\ge 0}$ both of the following may be convergent with different limits:

$$\begin{array}{rl}\sum _{i=0}^{\infty }\left(\sum _{j=0}^{\infty }{a}_{ij}\right)& =S_0+S_1+S_2+\dots \\ \sum _{j=0}^{\infty }\left(\sum _{i=0}^{\infty }{a}_{ij}\right)& =b_0+b_1+b_2+\dots \end{array}$$

${\sum }_{i,j\ge 0}{a}_{ij}$ is called a double series.

💡 ${\sum }_{k=0}^{\infty }{b}_k$ is a linear arrangement of the double series ${\sum }_{i,j\ge 0}^{\infty }{a}_{ij}$, if there exists a bijection

$$\sigma :\mathbb{N}⟶\mathbb{N}\times \mathbb{N}$$

with $b_k=a_{\sigma (k)}$.

📖 (Cauchy 1821).

Assume, there exists $B\ge 0$ such that

$$\sum _{i=0}^m\sum _{j=0}^m|a_{ij}|\le B\forall m\ge 0.$$

Then the following series converge absolutely:

$$S_i=\sum _{j=0}^{\infty }{a}_{ij}\forall i\ge 0\text{und}{U}_j=\sum _{i=0}^{\infty }{a}_{ij}\forall j\ge 0$$

as well as

$$\sum _{i=0}^{\infty }{S}_i\text{und}\sum _{j=0}^{\infty }{U}_j$$

and it holds that:

$$\sum _{i=0}^{\infty }{S}_i=\sum _{j=0}^{\infty }{U}_j$$

Also, every linear arrangement of the double series converges absolutely towards the same limit.

💡 The Cauchy-Product of the two series

$$\sum _{i=0}^{\infty }{a}_i,\sum _{j=0}^{\infty }{b}_j$$

is the series

$$\sum _{n=0}^{\infty }\left(\sum _{j=0}^n{a}_{n-j}{b}_j\right)=a_0{b}_0+(a_0{b}_1+a_1{b}_0)+(a_0{b}_2+a_1{b}_1+a_2{b}_0)+\dots$$

📖 If the series

$$\sum _{i=0}^{\infty }{a}_i,\sum _{j=0}^{\infty }{b}_j$$

converge absolutely, then their Cauchy product converges and the following holds:

$$\sum _{n=0}^{\infty }\left(\sum _{j=0}^n{a}_{n-j}{b}_j\right)=\left(\sum _{i=0}^{\infty }{a}_i\right)\left(\sum _{j=0}^{\infty }{b}_j\right)$$

📖 Let $f_n:\mathbb{N}⟶\mathbb{R}$ be a sequence. We assume, that:

1. $f(j)={\lim }_{n\to \infty }{f}_n(j)$ exists $\forall j\in \mathbb{N}.$
2. There exists a function $g:\mathbb{N}⟶[0,\infty )$, such that
   1. $|f_n(j)|\le g(j)\forall j\ge 0,\forall n\ge 0.$
   2. ${\sum }_{j=0}^{\infty }g(j)$ converges.

Then it follows that:

$$\sum _{j=0}^{\infty }f(j)=\underset{n\to \infty }{\lim }\sum _{j=0}^{\infty }{f}_n(j).$$

📎 For every $z\in \mathbb{C}$ the sequence $((1+\frac{z}{n}{)}^n{)}_{n\ge 1}$ converges and

$$\underset{n\to \infty }{\lim }(1+\frac{z}{n}{)}^n=\exp (z).$$