Hamiltonian Cycle in a Hypercube: Gray-Code
- Hamiltonian Cycle in a Hypercube: Gray-Code
- Gray-Code
- Motivation
- How to best arrange the holes on the disk
- Further Resources
Hamiltonian Cycle in a Hypercube: Gray-Code
Gray-Code

Motivation
Consider building a digital knob. Many such knobs today involve lights, a disk with holes attached to the knob and receptors on the other side. Depending on the orientation of the knob we can determine the currently selected value, the so-called Gray-code (named after Frank Gray). However, due to manufacturing imperfections this can cause transitions between the discrete values that are not smooth. Therefore, we want to have at max one single hole that changes from value to value to reduce the effect of such imperfections.
How to best arrange the holes on the disk
The most straight-forward way would of course be to punch holes into the disk in such a way that the arrangements of the holes represent the selected value in binary. However, then there are places where there are more than one hole changes between two discrete values, which would cause the transitional value to jump around all over the place. To get a scheme of holes for the disk where only one hole changes from value to value we can construct a so-called hypercube by assigning each vertex a value in binary such that no two neighboring vertices differ in more than one binary place (i.e., the hamming distance of two neighbors is exactly 1 for all pairs of neighboring vertices). We can start with a two-dimensional “hypercube”, which will give us 4 discrete values:
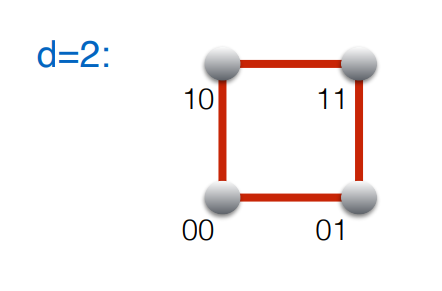
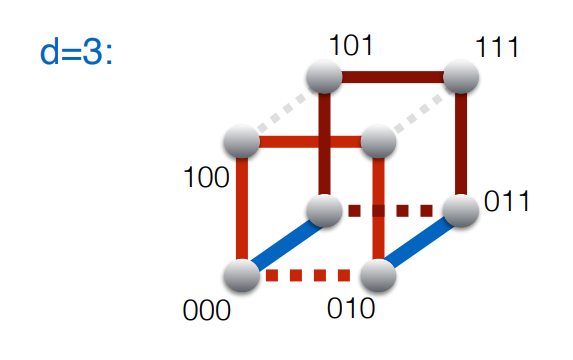
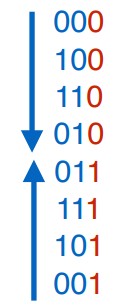
If we now move on to 3 dimensions we can create a cube in a similar fashion. We can take the two-dimensional “hypercube”, duplicate it by giving the existing vertices an extra binary place with the value 0 at the end and the new vertices an extra binary place with the value 1 at the end. We end up with the situation in the middle, in which a Hamiltonian cycle can easily be constructed as shown. Notice how the property that any two vertices connected by an edge are distinct by exactly one bit still holds true. If we look at the Hamiltonian cycles before and after the transformation we notice a simple pattern. We are walking the existing cycle “forwards”, then move to the duplicated part of the cube via a blue edge, then walk the duplicated part in backwards order of the existing part, and go back to the start via the other blue edge. We can thus construct a Hamiltonian path in a hypercube with the simple rule shown on the right, where the rule is: write down the order of the existing Hamiltonian path first forwards, then backwards (blue part), then add a 0 to the first half and a 1 to the second half (red part). You end up with a Hamiltonian path in a hypercube that is one dimension higher than what you started with. This works for arbitrary dimensions.
Using this technique we can arrange the holes on the disk of the knob in exactly the way of such a Hamiltonian cycle and we are guaranteed to only have one changing hole between any two neighboring discrete values. It ends up looking like the bottom right of the very first picture of this page.