RSA Public-Key Encryption

(Copied/paraphrased/annotated from the script on Discrete Mathematics HS21 by Prof. Ueli Maurer)

Motivation and Introduction

The RSA public-key cryptosystem, invented in 1977 by Rivest, Shamir, and Adleman (R. L. Rivest, A. Shamir, and L. Adleman, A method for obtaining digital signatures and publickey cryptosystems, Communications of the ACM, Vol. 21, No. 2, pp. 120–126, 1978.), is used in many security protocols on the Internet, for instance in TLS/SSL. Like the Diffie-Hellman protocol (Diffie-Hellman Key-Agreement) it allows two parties to communicate securely, even if the communication channel is insecure, provided only that they can authenticate each other’s public keys (respectively the Diffie-Hellman values). Moreover, the RSA system can be used as a digital signature scheme (see below). RSA was the first cryptographic system offering this important functionality.

$e$ -th Roots in a Group

Recall Lagrange’s theorem:

📖 Lagrange’s Theorem: Let $G$ be a finite group and let $H$ be a subgroup of $G$ . Then the order of $H$ divides the order of $G$ , i.e., $∣ H ∣$ divides $∣ G ∣$ .

To understand the RSA system, all we need is the following simple theorem which is a consequence of Lagrange’s theorem.

📖 $e$ -th Roots in a Group: Let $G$ be some finite group (multiplicatively written), and let $e \in Z$ be relatively prime to $∣ G ∣$ (i.e., $gcd (e, ∣ G ∣) = 1$ ). The function $x ⟼ x^{e}$ is a bijection and the (unique) $e$ -th root of $y \in G$ , namely $x \in G$ satisfying $x^{e} = y$ , is

$x = y^{d}$

where $d$ is the multiplicative inverse of $e$ modulo $∣ G ∣$ , i.e.,

$e d \equiv_{∣ G ∣} 1.$

Proof: We have $e d = k \cdot ∣ G ∣ + 1$ for some $k$ . Thus, for any $x \in G$ we have

$(x^{e})^{d} = x^{e d} = x^{k \cdot ∣ G ∣ + 1} = (x^{∣ G ∣})^{k} \cdot x = x$

$x^{∣ G ∣} = 1$ because of the following corollary we stated earlier:

📎 Let $G$ be a finite group. Then $a^{∣ G ∣} = e$ for every $a \in G$ .

This thus means that the function $y ⟼ y^{d}$ is the inverse function of the function $x ⟼ x^{e}$ (which is hence a bijection). Thus the theorem about $e$ -th roots in a group has been proven.

Description of RSA

Motivated by the Diffie-Hellman protocol also based on modular exponentiation, Rivest, Shamir and Adleman suggested as a possible class of groups the groups $Z_{n}^{*}$ , where $n = pq$ is the product of two sufficiently large secret primes $p$ and $q$ . Recall that $φ (n)$ is the Euler function mentioned earlier:

💡 The Euler function $φ : Z^{+} ⟶ Z$ is defined as the cardinality of $Z_{m}^{*}$ (known as Euler’s totient function or Euler’s phi function):

$φ (m) = ∣ Z_{m}^{*} ∣ .$

Also recall that its value can be computed using the prime factorization of its argument:

📌 If the prime factorization of $m$ is $m = \prod_{i = 1}^{r} p_{i}^{e_{i}}$ , then

$φ (m) = i = 1 \prod r (p_{i} - 1) p_{i}^{e_{i} - 1} .$

The order of $Z_{n}^{*}$ ,

$∣ Z_{n}^{*} ∣ = φ (n) = (p - 1) (q - 1),$

can thus only be computed if the prime factors $p$ and $q$ of $n$ are known. The (public) encryption transformation is defined by

$m ⟼ y = R_{n} (m^{e}),$

and the (secret) decryption transformation is defined by

$y ⟼ m = R_{n} (y^{d}),$

where $d$ can be computed according to

$e d \equiv_{(p - 1) (q - 1)} 1.$

The RSA public-key cryptosystem is summarized in the following figure. Note, that this is one-way only, Alice will receive an encrypted message from Bob and will be able to decrypt it. One would also need to mirror the setup to enable two-way encrypted communication also from Alice to Bob.

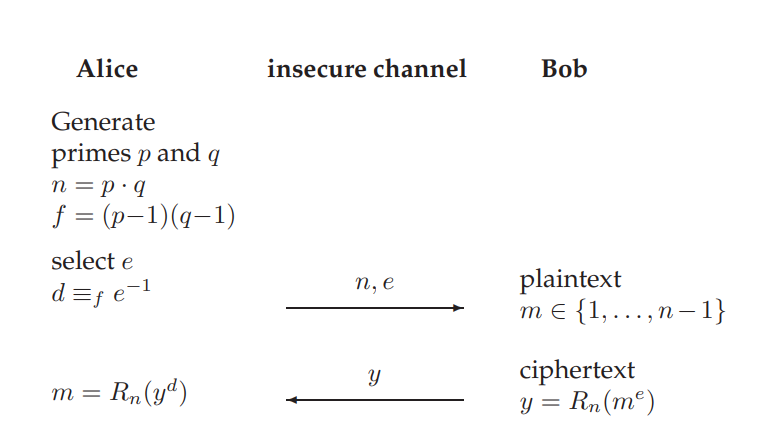
Untitled

The RSA system is usually (for instance in the TLS/SSL protocol) used only for key management, not for encrypting actual application data. The message $m$ is an encryption key (typically a short-term session key) for a conventional cryptosystem which is used to encrypt the actual application data (e.g. of a TLS session).

On the Security of RSA

Let us have a brief look at the security of the RSA public-key system. It is not known whether computing $e$ -th roots modulo $n$ (when $gcd (e, φ (n)) = 1$ ) is easier than factoring $n$ , but it is widely believed that the two problems are computationally equivalent. Factoring large integers is believed to be computationally infeasible. If no significant breakthrough in factoring is achieved and if processor speeds keep improving at the same rate as they are now (using the so-called Moore’s law), a modulus with 2048 bits appears to be secure for the next 15 years, and larger moduli (e.q. 8192 bits) are secure for a very long time.

Obviously, the system is insecure unless Bob can make sure he obtains the correct public key from Alice rather than a public key generated by an adversary and posted in the name of Alice. in other words, the public key must be sent from Alice to Bob via an authenticated channel. This is usually achieved (indirectly) by using a so-called public-key certificate signed by a trusted certification authority. One also uses the term public-key infrastructure (PKI).

It is important to point out that for a public-key system to be secure, the message must be randomized in an appropriate manner. Otherwise, when given an encrypted message, an adversary can check plaintext messages by encrypting them and comparing them with the given encrypted message. If the message space is small (e.g. a bit), then this would allow to efficiently break the system.

Digital Signatures

The RSA system can also be used for generating digital signatures. A digital signature can only be generated by the entity knowing the secret key, but it can be verified by anyone, e.g. by a judge, knowing the public key. Alice’s signature $s$ for a message $m$ is

$s = R_{n} (z^{d}) for z = m ∥ h (m),$