Lagrange Interpolation of Polynomials

(Copied/paraphrased/annotated from the script on Discrete Mathematics HS21 by Prof. Ueli Maurer)

Description

Recall the following lemma of polynomial algebra over fields:

📌 A polynomial $a (x) \in F [x]$ of degree at most $d$ is uniquely determined by any $d + 1$ values of $a (x)$ , i.e., by $a (α_{1}), \dots, a (α_{d + 1})$ for any distinct $α_{1}, \dots, α_{d + 1} \in F$ .

The proof for this lemma is constructive and exhibits a formula with which to construct a polynomial of degree $d$ from $d + 1$ values.

Proof of Lemma & Formula

Let $β_{i} = a (α_{i})$ for $i = 1, \dots, d + 1$ . Then $a (x)$ is given by Lagrange’s interpolation formula:

$a (x) = i = 1 \sum d + 1 β_{i} u_{i} (x),$

where the polynomial $u_{i} (x)$ is given by

$u_{i} (x) = \frac{( x - α _{1} ) \dots ( x - α _{i - 1} ) ( x - α _{i + 1} ) \dots ( x - α _{d + 1} )}{( α _{i} - α _{1} ) \dots ( α _{i} - α _{i - 1} ) ( α _{i} - α _{i + 1} ) \dots ( α _{i} - α _{d + 1} )} .$

Note that for $u_{i} (x)$ to be well-defined, all constant terms $α_{i} - α_{j}$ in the denominator must be invertible. This is guaranteed if $F$ is a field since $α_{i} - α_{j} \neq = 0$ for $i \neq = j$ . Note also that the denominator is simply a constant and hence $u_{i} (x)$ is indeed a polynomial of degree $d$ . It is easy to verify that $u_{i} (α_{i}) = 1$ and $u_{i} (a_{j}) = 0$ for $j \neq = i$ . Thus the polynomials $a (x)$ and $a (x) = \sum_{i = 1}^{d + 1} β_{i} u_{i} (x),$ agree when evaluated at any $α_{i}$ , for all $i$ . We note that $a (x)$ has degree at most $d$ .

It remains to prove the uniqueness. Suppose there is another polynomial $a^{'} (x)$ of degree at most $d$ such that $β_{i} = a^{'} (α_{i})$ for $i = 1, \dots, d + 1$ . Then $a (x) - a^{'} (x)$ is also a polynomial of degree at most $d$ , which according to the following theorem can have at most $d$ roots, unless it is 0.

📖 For a field $F$ , a nonzero polynomial $a (x) \in F [x]$ of degree $d$ has at most $d$ roots, counting multiplicities.

But $a (x) - a^{'} (x)$ has indeed the $d + 1$ roots $α_{1}, \dots, α_{d + 1}$ . Thus it must be 0, which implies $a (x) = a^{'} (x)$ . This concludes the proof.

Visualization

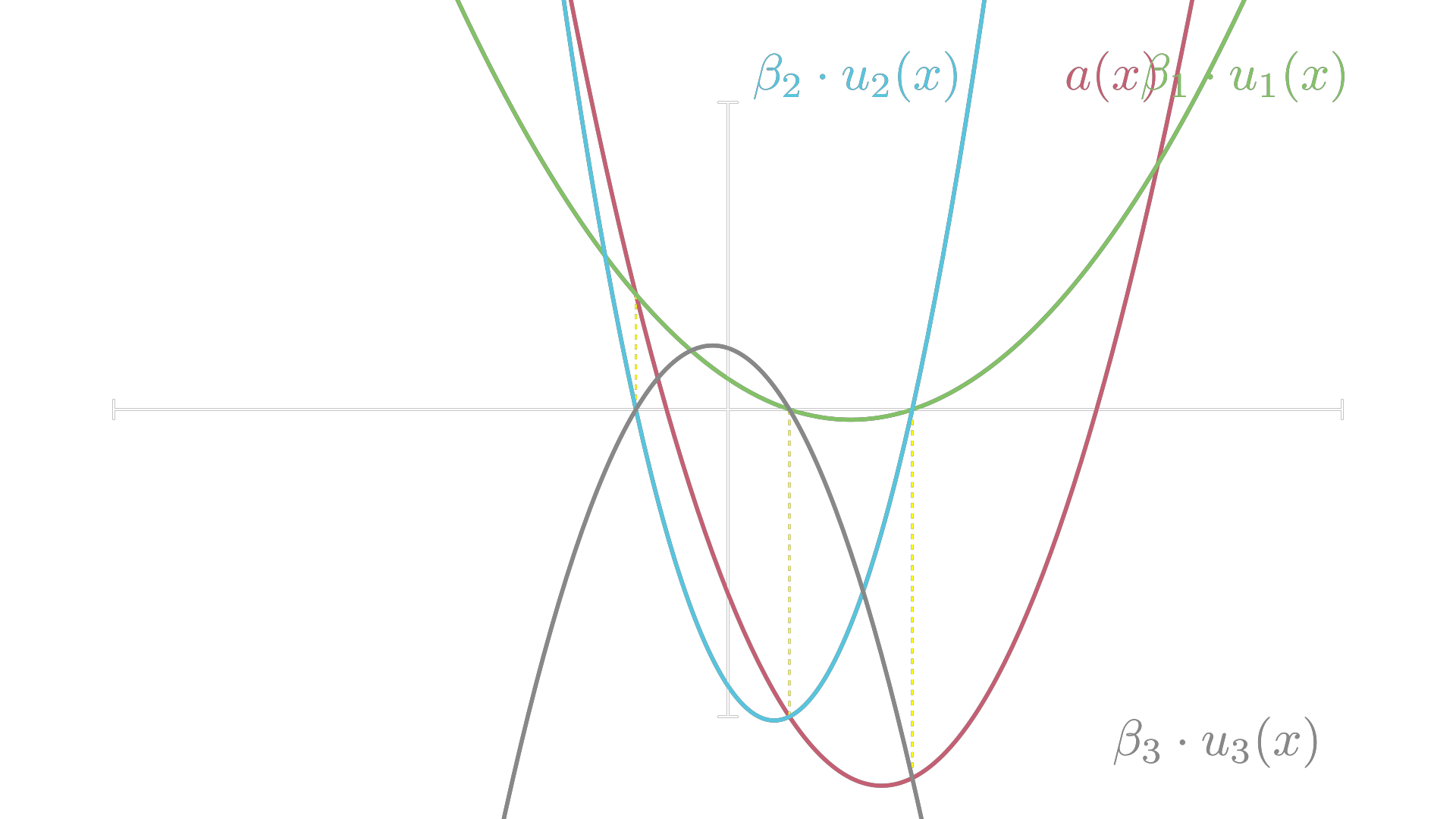
Visualized Lagrange-Interpolation for a polynomial of second degree.

In the visualization the polynomial $a (x)$ is computed by adding up all the other polynomials corresponding to the colored parabolas. These colored parabolas correspond to $β_{i} \cdot u_{i} (x)$ as above. They are computed Lagrange polynomials (as above), with $α_{1}, α_{2}, α_{3}$ given by the yellow arguments for $a (x)$ .

Further Resources

Lagrange polynomial - Wikipedia